Some basic probability and statistics for linguists

fall 2000.

The notion of a probabilistic model is a little more general that what follows immediately, but what follows is good enough for almost everything we care about in linguistics, at least for starters; so let's keep things simple, and say:

A probabilistic model consists of a universe of discrete, non-overlapping events, and a number (its probability) assigned to each such event. The probabilities are all non-negative, and the sum of the probabilities of the universe equals 1.0.

We can speak of the probability of a set of non-overlapping events, and its value is the sum of the probabilities of the events it contains. Such sets may be finite or infinite.

Some probabilistic models, which are especially interesting, have the property that all of the (discrete, non-overlapping) events are assigned the same probability. These models are said to have a uniform distribution. (Convince yourself that these models must have a finite number of events.) The probability of a set of events, in such a case, is directly proportional to the number of events in that set. The term distribution is used to refer to any set of (non-negative) numbers that add up to 1.0.

Example 1. The universe consists of all (single) tosses of a perfect die. There are 6 events in this universe, all with the same probability, 1/6.

Example 2. The universe consists of all (single) tosses of an imperfect die. There are 6 events in this universe, 5 with probabilities slightly under 1/6, and one with probability just over 1/6, such that these 6 numbers add up to 1.0.

Example 3. The universe consists of all sequences of 3 tosses of a perfect die. The events in this universe consists of the 216 sequences: 111, 112, 113, ….,211, 212,…,662, 663, 664, 665, 666. Each event has probability 1/216.

Example 4. The universe consists of all of the words in Tom Sawyer. The word the has probability 3,674/72,276; the word and has probability 3,071/72,276, etc., and the probabilities all add up to 72,276/72,276 = 1.0. This is not a uniform distribution.

Example 5. Like the previous example, but the probabilities are assigned slightly differently. There were 3,704 words which each have probability 1/72,706 assigned to them in example 4. In the next probability distribution, the probabilities are assigned as in probability distribution of example 3 for all words which appear 2 or more times in Tom Sawyer, but the probability is assigned to be 3,704/72,276 = .0512+ for any other string of letters.

What's the difference? What probability do the two systems assign to the word "computer"? or to the word "Weltanschauung"? Perhaps you can speculate on the probabilities that each of the two models would assign to the string of words found in Moby Dick (or any other book).

Example 6. The universe consists of all syntactic trees that obey a certain set of phrase-structure rules G. There is a probability assigned to each tree, and these probabilities add up to 1. (Remember, an infinite sum can add up to 1.0: for example, 0.9 + 0.09 + 0.009 + 0.0009 + … = 1.0) There are trees in this universe of all sizes, where "size" means the number of nodes in the tree: there are trees with just one node, with 2 nodes, etc. Let us denote the function which tells us how many trees there are with n nodes as #(n); there are #(1) trees with 1 node, #(2) with 2 nodes, and so forth. Then our probability assignment is this: a tree with n nodes in it is assigned a probability of 9*(0.1)ⁿ / #(n). That is, the probability is assigned uniformly to all the trees that have the same number of nodes -- but that's not a uniform distribution over the whole universe. Each "size" is assigned a total amount of probability equal to 9*(0.1)ⁿ, and then that probability "mass" is distributed uniformly over those trees, which are #(n) in number.

Example 7. The universe consists of all the ways of forming 2-word (ordered) pairs from the words in Tom Sawyer. These are called biwords or bigrams. For example, it contains the bigram of the, but also the bigram the of. The probability distribution assigned to each of these bigrams is based on the counts of the bigrams in Tom Sawyer. There are roughly 72,275 bigrams in Tom Sawyer. (How can that be "roughly"? You'll see.) of the is assigned probability 351/72,275, while the of is assigned probability 0.

Normalization: this is an important "trick" -- there's nothing illegitimate about it, though, even if I call it a trick. (It is especially important in the context of what's called a Boltzmann-Gibbs distribution, but we're not there yet.) Suppose you have a finite universe, and you assign a (nonnegative) number to each item in the universe based on anything you want. (Intuitively, though, the numbers should have the property that the bigger the number you assign to an element, the more likely you think it is.) You can add up the numbers you have assigned to all of items in the universe; that sum is usually called "Z". Then the probability distribution you have is this: the probability of each item is the number you have assigned it divided by Z. Clearly, it's a distribution, because all of these numbers are non-negative and they add up to 1 (convince yourself of that).

Note that the number could be something silly, like the page number on which the word appears in your Webster's Dictionary -- that is a non-negative number, after all. Or it could be the number of times it appears in Tom Sawyer (that would give us the distribution we looked at above). Or it could be the square of the number of times it appears in Tom Sawyer, or e raised to the power of the number of times it appears there. You can always sum and normalize ( = divided each value by the sum of all the values), and that will give you a distribution.

1. Sigma notation S; pi notation P: we'll use these everywhere, for sums and products.

2. The notion of a distribution: a set of numbers that add up to 1.0. This is the most basic notion. We must always be clear on what set of things we're talking about -- the universe, so to speak; and there must be a measure that we can talk about, and we must ensure that the measure of the whole set is 1.0, and that every set we care about has a measure that we can figure out, somehow; and that the measures of two independent sets is the sum of their measures.

3. Probability and weighted average. Real important, too: if there's some number (well, not a fixed number, but a function that maps to a number) that we can compute for some sets that we care about in the universe, then we want to be able to talk about the weighted average of that function -- and it's the measure that allows us to do that.

(skip 4.)

5. Logarithm: Base 2 logarithm (almost everywhere).

But first, base 10 logarithm: if you have a number of the form 1 followed by n 0's, that's 10 to the nth power; and its base 10 log is n.

Since log is continuous, this means for any number that is a simple 1 followed by n 0s, count the number of zeros ( to the left of the decimal point, if there is one), and that's the base 10 log. For any other number, the log is just the number of digits (to the left of the decimal point) plus some fraction less than 1.

The same is true for other log bases, if we shift to a notation using that base. We will care, much of the time, for base 2 notation.

Definition: if n = 10^k, then log (base 10) of n = k.

if n = 2^k, then log (base 2) of n = k.

Log ( a * b) = log (a) + log (b).

Log (1) = 0.

log (0) is not defined, but log (x) goes to -1 * infinity as x goes to 0. We'll always take n log n to be 0 if n=0. Go figure.

log (1/N) = - log (N);

log (a/b) = log (a) - log (b)

6. The number of yes/no questions it takes to describe a choice out of a set of N (equally likely) outcomes is log (base 2) of N.

That's the same thing as describing the case where we have equally likely outcomes, each of which has probability 1/N.

log (N) = -1 * log (1/N).

7. Suppose that the ratio of two sounds t and d is 1:1 in a certain environment. What is the information supplied by each of the sounds.

Suppose the ratio is 1 t to 10 d's. What is the information transmitted by each of them?

Suppose in a given environment there are only t's and no d's. How much information is given by learning that a t, not a d, has been transmitted?

8. If there are K possible segments in a given environment, the information of segment n is the same as the degree of its markedness.

9. Factorials: n! -- Stirling's formula; log n! ~ n log n; n (log n - 1); n (log n - 1) + 0.5*(log(n) + log (2pi)).

10. How many sentences of length n (n words) are there if there are N words in the lexicon, and the same word can appear twice in a sentence? What if no sentence can have the same word twice?

11.

12.

a. Consider the set of all sentences of length 1 word. Assign a probability to each such (mini-) sentence, based on some corpus. Those probabilities must add up to 1.0.

b. Consider the set of all sentence of length 2 words. Assign a probability to each such (mini-) sentence. Those probabilities must add up to 1.0. Take the probabilities for each word in case a, and multiply these probabilities for each word in the 2-word sentence. Can we convince ourselves that total will add up to 1.0?

c. If the sum of the probabilities of all of the words adds up to 1.0, what does the sum of the logs of the probabilities add up to? Be clear on this.

d. Go back to case b. What is the probability of the sentence "I see" in terms of the probability of "I" and "see"? What is the log probability of the sentence "I see" in terms of the log prob (I) and log prob (see) ? What is the relationship between log prob (I see) and log prob (see I)?

e. What is the probability of each letter in a given corpus? Compute those probabilities for each of the 27 letters in English (the 27^th covers everything not in the first 26).

f. What is the probability of the word "the" based on letter probabilities? Don't forget the spaces around "the". What is the probability of " eht "?

g. What is the relationship between the probability of "the" based on letter frequencies and based on word frequencies in the same corpus? The notion of frequency and probability is set against the background of a model.

h. What is the probability of the word "the" based on the letter probabilities chosen from different corpora of English? based on a corpus of French text? Based on a corpus of Latin text? How much information must be computed and retained to perform each of those three computations? How about the probabilities of the word "hoc" under those three models? How does this permit you to perform automatic language identification?

[i. Why do people think that probabilistic models involve fuzzy applications of criteria? (No correct answer to that question.)]

12. Suppose you have a category N, with a frequency distribution over the words in the category. There are <N> distinct words in the category, and each word n occurs with frequency [n] (that's just notation.).

If you pick 1 word from N, what are the chances it will be book? What are the chances it will not be book?

If you pick 2 words, what are the chances that both will be book? What are the chances that neither will be book? What are the chances that exactly 1 will be book?

If you pick 3 words, what are the chances that all three will be book? What are the chances that none will be book? What are the chances that exactly 1 will be book? Exactly 2?

If you only care about the split: book versus any word that isn't book, then if you're making n word-choices, then there are exactly 2ⁿ reality-paths you could pass through. Exactly 1 of them consists of choosing book each time, and exactly 1 consists of choosing book none of the time. n of them consist of choosing book exactly 1 time, and n consist of choosing book exactly n-1 times.

The chance of going through each path is determined if we know the probability of the word book. The path consisting of choosing book n times has probability [book]ⁿ. The path consisting of choosing book none of the times has probability ( 1 - [book] )ⁿ. A particular path that consists of n selections of the word book and N-n selections of some word other than book will be of probability [book]ⁿ * (1-[book]^N-n). How many such paths are there? If the answer to that question is K, then the probability of picking n copies of the word book in N tries is exactly K times [book]ⁿ * (1-[book]^N-n).

So: how many "selection paths" are there in which choice A is made n (let's say that's selecting the word book ) and choice A is not made the other (N-n) times? Don't think of it as if it happened sequentially in time -- think of there being N slots in a row, and n distinct copies (#1, #2, ..., #n) of the word book to be inserted in the slots. The first copy (book #1) can be placed in N different places; the second, in N-1 different places, and so on, down to the N-n+1 copy, which can go in N-n+1 different places. So the total number of different ways of doing that is the product of all those numbers = N!/(N-n)!. Now we go back and realize that we don't care about the numbering we put on those copies of the word book, so there are n! copies of the placements that we will treat as being the same. So the final answer is N!/(n! (N-n)!). This is extremely important and should become second nature.

And what, then, is the probability of the word book occurring n times in a corpus of N words, if book's probability is b = [book]? ( N! / (n! (N-n)! ) bⁿ (1-b)^N-b

Suppose there's a noun W which has a singular and a plural, and we expect a noun to be in the singular p of the time; let's say p = 0.8. If W occurs 100 times, which is the probability it will be singular in 80 of the cases?

N = 100, n = 80, b = .8. So the answer is ( 100!/ 20! 80!) * (.8)⁸⁰ (.2)²⁰. Great. How much is that?

Use Stirling's approximation to find the log of the probability. In fact, let's take the log of the formula we started with.

13. Conditional probability.

Conditional probability: if we care about some subset of the universe in which some condition C is true, we speak of conditional probability given C. If some part P of the universe that we care about is part of the universe in which C holds, and P's measure is m(P), then its conditional probability given C is m(P)/ m(C), which stands to reason, doesn't it? Remember that all measures are between 0 and 1, so dividing by a measure gives us a larger number. The measure of P is increased, in the context of the smaller universe we're considering momentarily.

More generally, we define the measure of A given B as the measure of the intersection of A and B, divided by the measure of B. P(A|B) = P(A and B) / P(B).

Notation: the probability of A given B is written prob (A | B) -- I'm using probability and measure here interchangeably (measure is the more general concept, but we only care about probability measures here).

a. If you choose a day from a year, what is the probability that you will choose a Tuesday, given no further knowledge of the selection procedure? What is the probability that you will choose a day in January? What is the probability that you will choose a day in the winter? If you know that the day chosen is in December, what is the probability that the day chosen is in the winter? If you know that the day chosen is in January, what is the probability that the day chosen is in the winter? If you know that the day chosen is in the winter, what is the probability that it is in January? In December? In July?

In a corpus of 100,000 words from Tom Swift, the occurs 4886 times. Following the, the highest scoring words were: young, 146; diamond, 97; cave 83; fire, 78; man, 78; airship 74; mountain, 61; secret, 53. Let us compare what the probabilities are of these words based on a model that assumes no connection between a word and what preceded it (a Bernoulli model) and also a model that assumes that a word's probability is based on what immediately preceded it (a Markov model). There are many Bernoulli and Markov models, but let's make a model based as heavily as possible on the observed statistics. Do that -- all you need are the following raw counts from this corpus:

young: 157; diamond, 122; fire 219; cave 140; man, 244; airship 138; mountain 152; secret 83;

[Let's try to maintain the convention that subscripts always indicate the left-to-right order of words, and superscripts can be used to mark particular lexical entries -- so w₁ always refers to the first word of a sequence, where as w¹ will refer to the first word in our lexicon, which might be "a" if it is alphabetized. We can if we like think of "w₁" as the name of a function that maps from sequences of words to word-types.]

Prob (young , given that the preceding word is the) = Prob (w_i = young | w_i-1 = the) =

146/4886.

Prob (the, given that the following word is young) = Prob (w_i = the | w_i+1 = young) = 146/ 157.

So what is the conditional probability of a word, given the preceding word?

Prob (w_i = young | w_i-1 = the) = # bigrams "the young" / # "the" = [the young]/[the].

Prob (w_i = the | w_i+1 = young) = [the young]/ [young].

14. What is the probability of a given sentence S?

S = {w_i, i = 1, ..., n}

If we use a Bernoulli model, there is no syntax (that's the definition...); hence prob (S) = prob(w₁)*prob(w₂)*...* prob (w_n).

What is the log probability of S, same model?
log prob (S) = log prob(w₁) + log prob(w₂) + ... + log prob (w_n).

Suppose we use a Markov model, which means that we model the probability of word w_n based only on itself and w_n-1.

prob (S) = prob( w¹ = w_n1 | w_n1 is the first word) * prob (w² = w_n2 | w¹ =w_n1 ) * ...

* prob (w^k = w_nk | w^k-1 =w_nk-1 )

And we normally make the assumption of a stationary Markov model, meaning that the conditions linking one word to the next are fixed once and for all, so the conditions (to the right of the vertical stroke) are independent of the choice of the superscript: one word conditions the next independent of where the pair are in the string.

prob (w² = w_n2 | w¹ =w_n1 ) = # bigrams (w^k_n1 w^k+1_n2) / # w_n1 = [w^k w^k+1] / [w^k ]

(just two different notations, there).

15. How do we compute how much better a job a Markov model is compared to a Bernoulli model? The natural way to do that is to take a real sentence, and compare the probabilities each assigns to it. Obviously (right?) the Markov model which tell us that the probability of the sentence is much higher than the Bernoulli model will.

16. Phonology. Suppose we model word/syllable phonology with a Bernoulli device that emits two symbols, s and #. Sequences of s's between #s are called words. prob (#) = p. (Why?)

Suppose p = 0.5. Then a typical sequence might be:

#s s # s # # s s s # s ##

Suppose p = 0.2. Then a typical sequence might be:

# s s s s s # s s s s # s s s s s s s # # s s s

(We could consider many alternatives, such as generating feet. We will return to this later.)

Let's stick with p = 0.5. What's the probability of a word having 3 syllables?

Suppose then that each syllable has probability Po of having an onset, Pn of having a nucleus, and Pc of having a coda. What is the probability of a CVCVCV word, given those parameters?

P(CVCVCV|#) = P(#SSS# | #) * Po³ * Pn³ * (1-Pc)³

and P(#SSS#) = (0.5)⁴

(I assume that this is computed "given initial word-boundary").

17. Bayes' Rule:

Let us suppose that we can speak of the probability of a hypothesis H. What is the probability of such a hypothesis H, given some data D? Experience and common sense would tell us that

The probability of a hypothesis H given some data D is proportional to the inherent likelihood of the hypothesis and (2) the degree to which the hypothesis H predicted the data D, and inversely proportional to the likelihood of the observed data. (The more likely the data, the less useful it is in changing the strength of our beliefs, right?).

This is formulated in Bayes' rule:

The simplest derivation comes from the definition of conditional probability:

, so

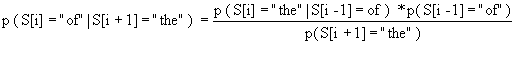
18. More exercises. (Sorry if there's some repetition.)

a. L = lexicon, |L| = L₀ = size of the lexicon. How many sentences are there of length n? How many, if no sentence has 2 instances of the same word?

b. P = set of phonemes in a language. How many words of length w₀ are possible if we know nothing about phonotactics ( = principles of allowed phoneme sequences)? How many if no word may have the same phoneme twice? How many distinct lexicons of size L₀ are there? How many words are possible of size less than or equal to length w₁? How many distinct lexicons are possible in such a language?

c. If C = set of consonants, of size C₀, and V = set of vowels, of size V₀, and all words are of length 2k and of form (CV)^k. How many words are there of length 2k?

d. Compare the sizes of the number of possible words in cases b and c by computing the log of the ratio of the sizes. Put it in a form that is comprensible.

e. Suppose all words are composed of syllables of the four OVC (onset-vowel-coda), and the number of possible onsets is C_o, the number of vowels is V₀, and the number of possible coda consonants is C_c. How many words of length 3k are there? What if the coda is optional – then how many are there? What if the coda and onset are both optional?

f. Suppose all words are made of a stem and a suffix. There are T stems and F suffixes in a language. How many possible words are there?

f. Suppose there are 10,000 ( = N₀) names in the directory at the European Union headquarters. There are F₀ distinct first names and L₀ distinct last names. (What inequalities do we already know?).

How many possible names could be created from the first and last names on the list, if we use the phrase-structure rule , etc? How many if we use the rule ?

What probability do we wish to assign to each first name, and what to each last name? What choices do we have? We will use these probabilities in the expansion , etc.

g. Describe the algorithm for computing the probability of the particular directory that in fact exists, based on the frequencies derived from that list. Assume that there is a category called List, and it expands to N₀ instances of the category Name. What is the probaiblity of that expansion? Assume a set of rules of the form .

Compute the probability of list (where N₀ = 3) John Smith, Mary Smith, Jacques Dupont. Now compute the probability of that list, if we make the convention that all lists are by definition alphabetized. (That decision means that the probability of a given list in the new sense is the sum of the probabilities of the lists in the old sense that had the same names on it. How many were there?). Extend the results to the general case of N₀ words.

h. Now consider the possibility of enhancing the grammar by creating 30 new categories, of the form

: N_English, N_French, etc. (10 of those, for 10 language), plus 10 categories of first names (one for each language), and 10 categories of last names.

Write the new rules, and explain how to assign probabilities to the new categories. There is more than one way to do this. Suppose there are no occurrences of the first name Jacques among the English family names. Do we wish to assign a 0.0 probability to the expansion F_english -> Jacques ? What works better if we do, and what works worse? (probability of the data; success in the future with this model).

In what sense does this increase in category size lead to a more accurate grammar? Be absolutely sure that you can quantify this accuracy.

19. Unigram and bigram models.

Suppose we have a lexicon L with N words, each word assigned a probability p(w_i);

S p(wⁱ)=1. We can think of the probabilities as forming a vector W, of length N (i.e., W lives in a space of dimension N, and its coordinates are all non-negative, and they add up to 1.0. What kind of surface is it composed of points whose coordinates add up to 1.0? Is it flat or curved?). Each dimension of that space is associated with a particular word in the lexicon L. The i^th dimension is associated with word wⁱ.

A word wⁱ can then be associated with a vector wⁱ consisting of all 0s except for a 1 in the i^th place. Its probability is then W.v. Remember that the "dot product" of two vectors (which must be of the same dimensionality = length) is calculated by multiplying the corresponding coefficients (= components) of each and then adding those altogether.

Instead of storing probabilities in the vector W, we store log probabilities and we call this new vector LogW. Then suppose we have a sequence of word-vectors vⁱ; the log probability of the sequence on a unigram model is LogW. vⁱ

Suppose you have a vocabulary: cat, dog, saw, the with probabilities 0.25 each. What does the probability vector look like? What does the log probability vector look like? How about the inverse log prob vector? What is the probability it assigns to the sentence "the cat saw the dog"? and "the dog saw the cat"? and "the the dog cat saw"? What are the probabilities if the probabilities assigned to the words are (respectively) .2, .2, .2, .4? What is the largest probability you can assign to "the dog saw the cat" under a unigram (bernoulli) model? Express that in log prob, and connect up with information content.

What if we have a bigram model in which the prob of dog|the = .5 and cat|the = .5 and all the rest are as before. Draw a big*ram chart:

	`the	dog	cat	saw
the	0	.5	.5	0
dog	.25	.25	.25	.25
cat	.25	.25	.25	.25
saw	.25	.25	.25	.25

What is the probability now of "the dog saw the cat," "the cat saw the dog," and "the the dog cat saw"? How about "the dog the cat saw"?

Now suppose we want to develop a bigram model, where the probability of a given word is dependent on the previous word. We will store all these probaiblities in a matrix B: b_i,j is the probability of word w_j immediately following the word w_i.

All utterances that we care about will be defined to begin with a special symbol # and end with that symbol also, and # will occur nowhere else in an utterance.

w_i represents a particular word in the lexicon. w^j represents the j^th word (phoneme) in an utterance. We'll push notation a bit and frequently write w^j_m, and that will normally mean the index number of the jth word in the sequence, or loosely, just the jth word in the sequence, while allowing us to link the subscript to another occurrence of that variable in a formula. (This is to avoid complicating the formula with Kronecker deltas).

Talking about Viterbi and Forward computations with matrix representations of Markov models. Word categories as symmetries.

N = number of states

z = length of sentence in question

We will break up our Markov model into a set of matrices G_w (G for grammar); each G is an NxN matrix, where N is the number of states in our model. This matrix is just for emitting (or accepting) a particular word. Its elements are (g_i,j), which represents the probability of making the transition to state_j from state_i — while emitting this (or accepting) word w.

We have to make a decision about how to treat probability mass. I will try it this way: the probability mass over all of the G_w's sum to 1.0. The probability mass in G_w is prob(w), which can be estimated empirically (if one wants) but doesn't need to be. No other conditions need to be met.

We thought (in class) that we might want to impose a Markov-style assumption like that the sum of the probabilities from a given state, summing over all possible words and all possible target states, should add to 1.0. That would make each "panel" sum to 1. But I don't see what's gained by imposing that; that means summing over all possible words coming out of a state, and we're usually not interested in that collection.

Now we can say (as on the next page) that two word-matrices can be multiples one of another.

A state S is a vector in a space of N dimensions. It is a distribution, so its entries sum to 1. A pure state has a coordinate of value 1. Any other state is a mixed state.

A sentence Z is a string of words: Z = w¹ w² … w^z. We want to generate a set of strings of states; each string will be n states long, and there will be n of them, one for each state.

Let’s call a set of such strings, each associated with a number between 1 and N, a Viterbi set V, and speak of the length of V in the obvious sense.

So now we have a sentence Z = w¹ w² … w^z. That string of words allows us naturally to talk about a corresponding set of matrices G¹ G² … G^z , where Gⁱ is G_wi, the matrix for word wⁱ.

What we want to do is to start out with the right initial state S₀ (which has a 1 in the coefficient for the state in which the Markov models must begin), and then multiply it by the string of grammars G¹ G² … G^z . The output is the final state S_F.

If our goal is to compute the Forward function, we’re actually done, if we use ordinary matrix multiplication. We can compute the probability of sentence Z as the sum of the components of S_F.

If our goal is to compute the best Viterbi path, we must define the Viterbi Max relation, which holds of 5 objects: two states, S₁ and S₂, two Viterbi sets V₁ and V₂ (where the length of V₂ = length of V₁ + 1), and an appropriate matrix G. The condition on V₁ and V₂ is that for all k, . (That is, S₂(k) gives the highest probability associated with a transition from a state in S_i to state k, and it observes that the transition came from state j.) The condition on the Viterbi sets is then that , where the j,k are as in the previous condition. This defines Max (S1, S2, V1, V2, G), which we might write more perspicuously as . Recall that G is a matrix for a particular word.

We can extend this to a whole sentence Z = w¹ w² … w^z, and we say that in the straight-forward way, which we will abbreviate as . Maybe we should write this G_Z(S₁) = S_z. We should convince ourselves that for fixed Z, this operator is linear, so that G_Z(aS₁ + bS₂) = aG_Z(S₁) + bG_Z(S₂). (What’s the point of that? To underscore the point that we can think about mixed states of the markov model as well as pure.)

That expresses formally the relationship between the initial state of the Markov model and the final state. The Viterbi-best path is then that path j in the Viterbi set corresponding to the (not necessarily unique) largest value S_n(j). We also call that value the Viterbi probability of the sentence. It must be less than the “real” probability, obviously.

Define the Backward function in like manner.

Symmetries

Can we say anything about the relationship between the states of a model and the words? What about the relationship between the number of states S, the number of words N, and the number of distinct matrices G_w? If all of the entries in a given row are the same in each of our matrices, then we have a model of the sort that Charniak told us to prefer: the word-probabilities are tied to the source-state, and independent of the target state.

In general, we certainly would be happier with fewer rather than more parameters, but what other ways would there be to have fewer than the maximum number of parameters (what is the maximum?).

The most linguistically natural way to reduce the number of free parameters is to see whether some pairs of the G_w matrices are multiples one of the other: G_i = l G_j. What would this mean? It would mean that other than the inherent probability of the two words being different (if lambda is not 1.0), the two words’ behavior is identical: which is what linguists mean when they say that the two words are in the same category.

What we see thus is that we can say define an equivalence relationship on words of being-in-the-same-category if their matrices are multiples of each other. Suppose we have two words, w1 and w2 and G₁ = l G_2. It is not difficult to see that if we taken one Z1 that contains w1, and convert it to Z2 in which we have replaced w₁ by w₂, then the ratio . (Is that true for Viterbi probability as well? — yes). Thus permutation of words preserves probability of sentences, up to a difference of a factor of lⁿ, where l is as defined and n is the number of occurrences permuted in the sentence. This is significant.

Null transitions

Let’s imagine a model in which the words could be null. Then the states could be more abstract, in the following sense.

When the words cannot be null, it is natural to think of the states as representing some crude sort of lexical category. But if some categories have only null outputs associated with them, then we can have nodes S, NP1, N, NP2, VP1, V, VP2, and S2; and we could associate non-null probabilities with only N and V if we chose to, while the transitions from S to NP1, NP1 to N, N to NP2, NP2 to VP1, VP1 to V, V to VP2, and VP2 to S2 could be quite large (even 1.0, if we chose).

The disadvantage of reconstructing phrase-structure this way is that (a) we multiply state-nodes: each phrase-structure node gets transformed into two nodes (X1 and X2), and (b) we multiply nodes: each phrase-structure node (or pair of nodes) is also copied for each place in the sentence it appears (e.g., NP in subject, NP inside PP). To some extent these multiplications can be handled (if that’s the word) by discovering, or imposing, symmetries, but in a different sense than above. Above we considered symmetries under permutation of words; here we consider symmetries under permutation of nodes.

There are two kinds of permutation (symmetry) to consider: symmetry of terminal (lexical) nodes, and permutation of non-terminal nodes. We can’t do the easy thing, which is to ask if simply permuting two nodes leaves the system unchanged. Note that permuting two nodes is easily formalized as multiplying by a matrix which is I (the identity) everywhere except for the interchange of two column m and n. Call that R(m,n). Suppose two lexical nodes M and N are effectively identical. This doesn’t means that for all grammar matrices, columns f and g are identical, and rows f and g are identical (that would be too easy). It means that for all grammar matrices G, if you interchange the input columns for M and N (call them m and n) and the output rows (s and t), then what you get is the same as the original . We can think of this as a “rotation” (that’s why “R”) of the matrix in which the four axes are interchanged, and then switched back.

Note that as regards computational implementation, we can precompute all sequences of matrices which have non-zero entries and which correspond to zero outputs (e.g., ). Why keep these steps distinct, then? Because it is these steps which display the symmetries which we need to keep explicit.

Minimum Description Length

How long is the description of a Markov model? Symmetries are the major way in which description length is kept small.